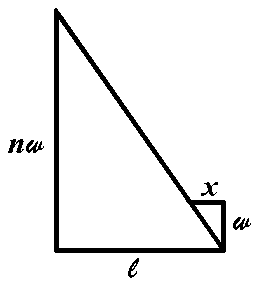How to cut a brick in thirds
This problem came about when I was building a patio, and needed to brick up a curved section. I didnít want to use half-bricks, since the curve was too tight and the gaps between the outside edges of the bricks wouldíve been too wide. But cutting bricks in fourths made the pieces so small, it looked I was trying to pave using oversize rocks! Cutting the brick in thirds was almost perfect, but I had a little delay while trying to figure out where exactly to cut the bricks to get perfect thirds. (Well, you tell me off the top of your head where to measure and cut a 7-3/4Ē brick to get it in thirds, allowing for a 3/16Ē saw blade kerf!)
What happened was, I discovered this little trick, which I havenít been able to find
anywhere else. Maybe I invented it, or maybe itís a masonís trick
thatís been around since the Egyptians, I donít know. But it was
cool enough to share with people, and Iíd sure appreciate some feedback from any masons out there who can tell
me that this is either cool or ho-hum.
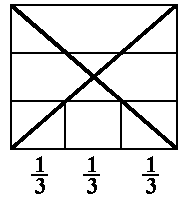
Our problem is to take a brick of given length (l) and
width (w),
and mark it so that the mark is exactly 1/3 of the way for the
edge along the long side. What I found was that, no matter
what the width of the brick is, if you stack up three of them (lay them together on the ground, I mean), and draw
a line from corner to corner, the point where that line hits the bottom brick first is at the desired 1/3 point!
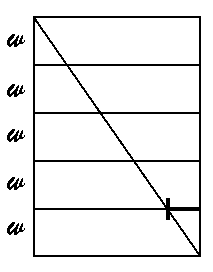
Not only that, but if you want to cut it in 5ths, 7ths, or any other fraction, just
stack up that many bricks (5 for 5ths, see below), and draw the same corner-to-corner line.
The mark you make on the top edge of the bottom brick is exactly that fraction of the whole length. (Of course, this would work for boards as well as bricks.)
Thatís it. Do I have something cool here, or is this a big fat who cares? Hereís the geometry proof, for those of you who care, but itís really straightforward.
Consider the figure Iíve drawn below, where there are 5 bricks stacked up.
I drew 5, but Iíll do the proof in general, for n
bricks. Iíve drawn two triangles in bold, which youíll see are similar. (Theyíre both right, and their vertex angles are congruent by alternate
interior, so AA similarity.) These triangles are shown below, drawn
by themselves, with the height of the big triangle being nw
to represent n bricks.
OR
With this picture, weíre done, because the similarity proportion is ![]() ,
,
and this simplifies to
.